前文我们探讨了树状数组的原理。树状数组就是一种数据结构,它天生用来维护数组的前缀和,从而可以快速求得某一个区间的和,并支持对元素的值进行修改。但是树状数组并非只有这一种功能,变形后它还能衍生出两个功能,本文我们就来分别讨论下树状数组这三大功能。
永远要记住,基本的树状数组维护的是数组的前缀和,所有的区间求值都可以转化成用 sum[m]-sum[n-1] 来解,这点无论是在改点还是接下来要说的改段中都非常重要。
这也是树状数组的基本应用。我们可以来看一下这道题 敌兵布阵。
如果看了前文 【前端也要学点数据结构】 神奇的树状数组,解法也就呼之欲出了,直接给出代码:
#include<iostream>#include<cstdio>#include<cstring>#include<string>using namespace std;#define N 50005int lowbit(int x) { return x & (-x); }int sum[N], cnt;void update(int index, int val) { for (int i = index; i <= cnt; i += lowbit(i)) sum[i] += val;}int getSum(int index) { int ans = 0; for (int i = index; i; i -= lowbit(i)) ans += sum[i]; return ans;}int main() { string str; int n, m, t, tmp, cas = 1; scanf("%d", &t); while (t--) { memset(sum, 0, sizeof(sum)); scanf("%d", &cnt); for (int i = 1; i <= cnt; i++) { scanf("%d", &tmp); update(i, tmp); } printf("Case %d:n", cas++); while (cin >> str) { if (str == "End") break; scanf("%d%d", &n, &m); if (str == "Query") printf("%dn", getSum(m) - getSum(n - 1)); else if (str == "Add") update(n, m); else update(n, -m); } } return 0;}改段求点和改点求段恰好相反,比如有一个数组 a = [x, 0, 0, 0, 0, 0, 0, 0, 0, 0],每次的修改都是一段,比如让 a[1]~a[5] 中每个元素都加上10,让 a[6]~a[9] 中每个元素都减去2,求任意的元素的值。
看例题 Color the ball
跟改点求段不同,这里要转变一个思想。在改点求段中,sum[i]表示Ci节点所管辖的子节点的元素和,而在改段求点中,sum[i]表示Ci所管辖子节点的批量统一增量。
还是看这个经典的图:
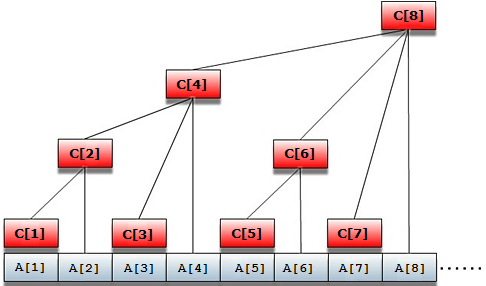
比方说,C8管辖A1~A8这8个节点,如果A1~A8每个都染色一次,因为前面说了sum[i]表示i所管辖子节点的统一增量,那么也就是 sum[8]+=1,A5~A7都染色两次,也就是 sum[6] +=2, sum[7] +=2 。如果要求A1被染色的次数,C8是能管辖到A1的,也就是说sum[8]的值和A1被染色的次数有关,仔细想想,也就是把能管辖到A1的父节点的sum值累积起来即可。两个过程正好和改点求段相反。
完整代码:
#include<iostream>#include<cstdio>#include<cstring>#include<string>using namespace std;#define N 100005int sum[N], n;int lowbit(int x) { return x & (-x); }void update(int index, int val) { while (index) { sum[index] += val; index -= lowbit(index); }}int query(int index) { int ans = 0; while (index <= n) { ans += sum[index]; index += lowbit(index); } return ans;}int main() { int x, y; while (scanf("%d", &n) && n) { memset(sum, 0, sizeof(sum)); for (int i = 1; i <= n; i++) { scanf("%d%d", &x, &y); update(y, 1); update(x - 1, -1); } for (int i = 1; i < n; i++) printf("%d ", query(i)); printf("%dn", query(n)); } return 0;}改段求段也有道经典的模板题:A Simple Problem with Integers
我们还是从简单的例子入手,比如有如下数组(a[1]=1,..a[9]=9):
1 2 3 4 5 6 7 8 9 10假设我们将 a[1]~a[4] 这段增加5,对于我们要求的区间和来说,要么是 [1,2] 这种属于所改段的子区间,要么是 [1,8] 这种属于所改段的父区间(前面说了,所有的区间求值都可以用sum[m]-sum[n-1]来解,所以我们只考虑前缀和),我们分别讨论。
如果所求是类似 [1,8] 这种,我们可以很开心地发现,我们将区间增量(4*5)全部加在 a[4] 这个元素上,对结果并没有什么影响!于是变成了一般的改点求段。
如果所求是类似 [1,2] 这种,我们可以用类似改段求点中染色的思想进行处理。譬如 [1,4] 成段加5,如果我们要计算 [1,2] 的和。我们将 [1,3] 进行“染色”(节点4加上了4*5的权重),因为 [1,3] 在树状数组的划分中可以分为两个区间,[1,2] 和 [3,3],所以我们用类似改段求点对这两块区域进行“染色”,染上的次数为5。我们要求的是 [1,2] 的区间和,我们只需找 2 被染色的次数,因为 [1,n] 进行染色。如果m(1<=m<=n)被染色,那么m的右边肯定都被染色了。求出被染色的次数,然后乘上区间宽度,就是整段的和了。
这样我们分别对两种情况进行了处理,更重要的是,这两种情况互不影响! 于是我们简单地把两个结果相加就ok了,而这两个过程,分别正是改点求段和改段求点!
完整代码:
#include<iostream>#include<cstdio>#include<cstring>using namespace std;#define N 100005#define ll __int64ll b[N], c[N];int n;int lowbit(int x) { return x & (-x);} void update_backwards(int index, ll val) { for (int i = index; i <= n; i += lowbit(i)) b[i] += val;}void update_forward(int index, ll val) { for (int i = index; i; i -= lowbit(i)) c[i] += val;}void update(int index, ll val) { update_backwards(index, index * val); update_forward(index - 1, val);}ll query_forward(int index) { ll ans = 0; for (int i = index; i; i -= lowbit(i)) ans += b[i]; return ans;}ll query_backwards(int index) { ll ans = 0; for (int i = index; i <= n; i += lowbit(i)) ans += c[i]; return ans;}ll query(int index) { return query_forward(index) + query_backwards(index) * index;}//---------------- main -------------- //int main() { int t, x, y; ll z; char str[2]; memset(b, 0, sizeof(b)); memset(c, 0, sizeof(c)); scanf("%d%d", &n, &t); n += 1; for (int i = 1; i < n; i++) { scanf("%I64d", &z); x = i + 1, y = i + 1; update(y, z); update(x - 1, -z); } while (t--) { scanf("%s", str); if (str[0] == 'C') { scanf("%d%d%I64d", &x, &y, &z); x += 1, y += 1; update(y, z); update(x - 1, -z); } else { scanf("%d%d", &x, &y); x += 1, y += 1; printf("%I64dn", query(y) - query(x - 1)); } } return 0;}这里有一点需要注意:一般的用数组数组来解的题,都是不用a[0]的,也就是元素是从a[1]~a[n],因为 sum[n~m]=sum[m]-sum[n-1],避免 n-1 为负数。而本题中的改段求段中的元素是从 a[2]~a[n+1] ,因为 update()函数中的子函数 update_forward() 函数中 index-1 不能为负,所以参数 index 最小是1,所以 sum[n-1] 中 n-1最小是1,所以n最小是2,所以元素下标必须从 2 开始。